I've always had a bit of a love for die-drop tables. You can do a lot of clever things with them, as they give you several dimensions of data at once and also leave room for interpretation.
When the dice fall on a chart, you have spacial information about where they have fallen, their position relative to each other, various axis of scalar values that might be the size, colour, and face-value of each die.
This lets you do some clever things like drawing procedurally generated maps from a simple set of rules, or quickly determining all sorts of things like a character's appearance or personality, details about locations, or anything you might cook up.
For my May 2019 micro-game submission to OMGAM, I had decided to make a die-drop derived game. Since Fudge dice were still my theme of 2019, I'd be dropping Fudge dice and using those values to somehow play a game.
When thinking about how to implement this, my mind kept wandering back to Conway's Game of Life which I played with for countless hours as a child. The basic premise was that, with simple rules, cells placed on a grid would replicate, grow, or die of either isolation or overcrowding.
These simple rules let you make all kinds of complex structures. You could create cellular automata that would act like pulsars, gliders, or eaters. Emergent behaviour and patterns would rise up from very simple data sets and rules.
I imagined an implementation where dice could be dropped onto a grid to establish the initial state of the game, and a player could manipulate the play field and manually iterate each step of the evolution process. This was obviously a little too complicated to represent in a micro-game.
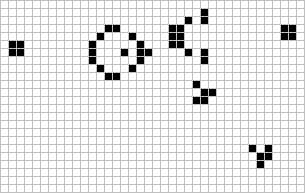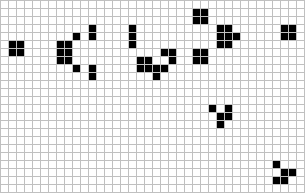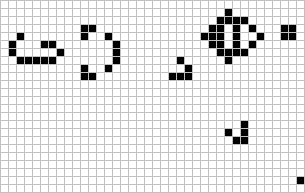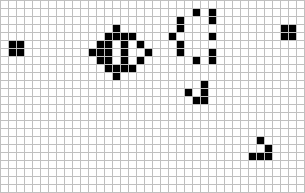
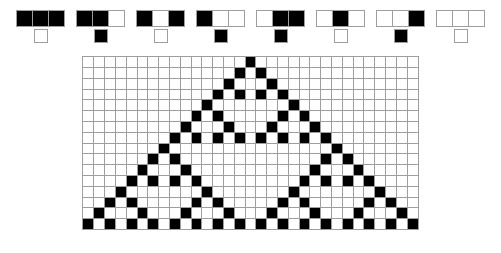
Researching more about other forms of cellular automata, I discovered that John von Neumann and Stanislaw Ulam had designed one-dimensional or "elementary cellular automata", later refined by Stephen Wolfram into simple rule sets that were fairly easy to evaluate by hand.
Instead of cells on square a grid, like in Conway's Game of Life, these were cells on a single line. The rules could be very simple, and each evolution of the game board could be easily figured on pencil and paper. The starting state of the board determined by how dice fell onto it.
All I needed was an objective to make it a game, instead of a toy.
I considered implementing a SIR model, which might be useful for a game about epidemics or zombie outbreaks. After some consideration though, what I came up with was Lemmings.
The objective would be to shepherd cells from one end of the line to the other, getting them past various obstacles. The obstacles would be determined by how dice fell, and the behavior of the obstacles would be determined by the face value of the dice.
Since some game conditions would allow for an infinite number of "lemmings" to reach the exit, I set a limit of thirty turns.
The end result of all this was 2dF Drop Cellular Automata Lemmingslike which ... I have to be totally honest, if you're not interested in turning yourself into a computer to evaluate the steps of an elementary cellular automation program, you probably don't want to try to play this. I had someone who knits take a look at this, and they weren't impressed even though knitting is basically the same thing.
I think it is fascinating though. Maybe I wont spend hours playing the game, but it provides some useful perspective to think about what games are and how they are played.
For me, the combination of rules and objectives are what make this a "game", as contrasted with a "toy" or a "play" activity.
Does that make a Rubik's Cube a "game"? I would say only when you manipulate it towards a goal. The device its self is a toy. If you don't set out to solve the puzzle and just spin the sides randomly, it is just playing with a toy. The act of moving towards a goal within the constraints of the device makes it a game.
Conway's Game of Life is a toy. If I challenge you to use it to make a self-replicating pattern with as few cells as possible, it just became a game. You can read Yifan Liu talk about similar concepts with more eloquent language.
When I think of this 2dFCAL as a game and how it relates to other game design, I think of how the rules of the activity shape how the player engages with the objective. If the player just drops dice onto the paper and iterates the cellular automation for thirty steps, they're playing with a toy.
But if they interact with the systems laid out in the game, they find ways to circumvent obstacles and avoid hazards. They can use obstacles to block hazards, and to shepherd their little creatures safely towards the goal.
The rules shape the way the player experiences the game. The system matters. A different rule set for processing the cellular automation would create an entirely different experience. The ways the player interacts with those rules and systems creates emergent situations.
This is a fairly extreme example of a highly structured set of rules applied to a codified goal, but I think that it directly overlaps with the more generalized table-top RPG play space. Specific rules craft specific experiences. Sometimes those rules create sandboxes, sometimes those rules create strict genre emulation. Always, they should be designed with intention.



No comments:
Post a Comment